

If you don’t want to, here’s the regression summary: We have used it in a previous tutorial so if you want to keep track of what we are talking about, make sure you check it out. However, this may still account for less than 50% of the variability of income. It may depend on your household income (including your parents and spouse), your education, years of experience, country you are living in, and languages you speak. It depends on the complexity of the topic and how many variables are believed to be in play. There, an R-squared of 0.2, or 20% of the variability explained by the model, would be fantastic. However, in social sciences, such as economics, finance, and psychology the situation is different. In fields such as physics and chemistry, scientists are usually looking for regressions with R-squared between 0.7 and 0.99. Unfortunately, there is no definite answer to that. The immediate question you may be asking: “What is a good R-squared? When do I know, for sure, that my regression is good enough?” What we usually observe are values ranging from 0.2 to 0.9.
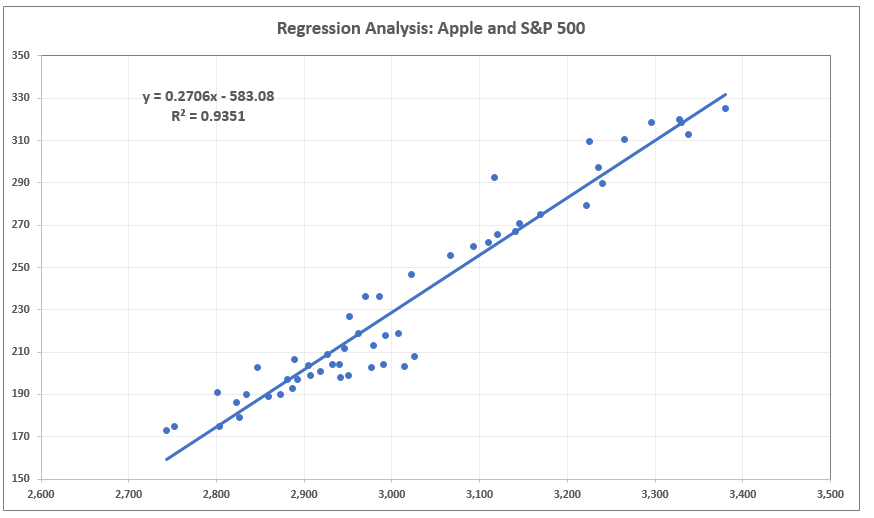

Unfortunately, regressions explaining the entire variability are rare. An R-squared of zero means our regression line explains none of the variability of the data.Īn R-squared of 1 would mean our model explains the entire variability of the data. It is a relative measure and takes values ranging from 0 to 1. It is equal to variability explained by the regression, divided by total variability. The R-squared is an intuitive and practical tool, when in the right hands. Now, it’s time to introduce you to the R-squared. A prerequisite to understanding the math behind the R-squared is the decomposition of the total variability of the observed data into explained and unexplained.Ī key highlight from that decomposition is that the smaller the regression error, the better the regression. If you are looking for a widely-used measure that describes how powerful a regression is, the R-squared will be your cup of tea.


 0 kommentar(er)
0 kommentar(er)
